Java'da Diziyi Özyinelemeli Toplama: 9 Adım

2025 Yazar: John Day | [email protected]. Son düzenleme: 2025-01-23 15:13

Özyineleme, çok az kodla bir sorunu hızla çözebilen çok kullanışlı ve zaman açısından verimli bir prosedürdür. Özyineleme, orijinal sorunu kısaltarak kendi kendine çağırarak oluşturduğunuz yöntemi içerir.

Bu örnek için, 10 tam sayıdan oluşan bir dizi toplayacağız, ancak boyut herhangi bir uzunlukta olabilir.

Gereçler

Temel Java sözdizimini bilmeli ve bu görev için kodunuzu yazmak için IDE'nize veya bir metin düzenleyiciye sahip olmalısınız.

Adım 1: Ana Yönteminizi Ayarlayın

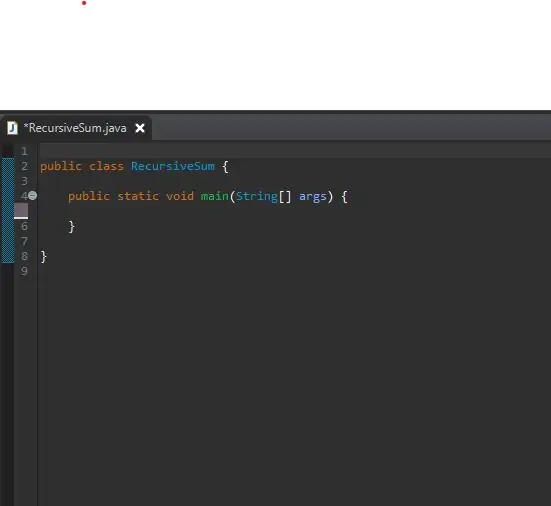
Başlamak için, ana yönteminizi yeni oluşturulan bir sınıfta ayarlayın. Sınıfımı RecursiveSum olarak adlandırdım. Burası tamsayı dizisini oluşturacağınız ve özyinelemeli yönteminizi çağıracağınız yerdir.

Adım 2: Özyinelemeli Yöntem Başlığınızı Oluşturun

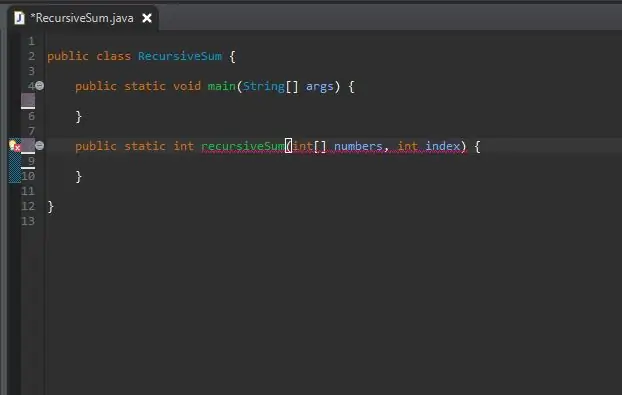
Ana yönteminizin dışında, özyinelemeli yönteminiz için yöntem başlığını oluşturun.

Yöntem, üzerinde kullanmak için bir nesne gerektirmeyeceği için statiktir.

Dönüş türü int'dir, çünkü kullanacağımız dizi tamsayılarla dolu olacaktır. Ancak bu, dizinin içerdiği sayı türü ne olursa olsun değiştirilebilir.

İki parametre alacak olan yöntemime recursiveSum adını verdim; bir tamsayı dizisi ve toplama ekleyeceğimiz dizin. Bu parametreleri sırasıyla sayılar ve indeks olarak adlandırdım.

Şu anda hataları göreceksiniz ve bu iyi. Daha sonra düzeltileceklerdir.

3. Adım: Kicker/Temel Durumunuzu Oluşturun

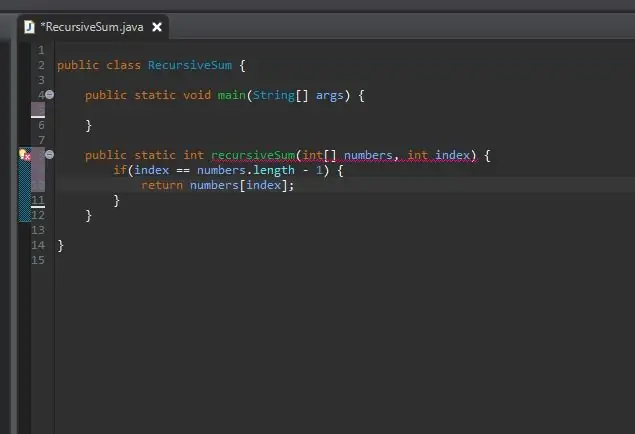
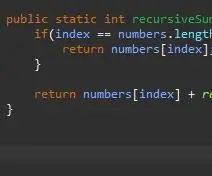
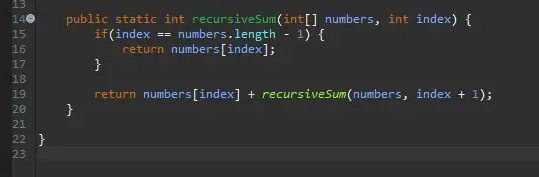
Özyinelemeli bir yöntem, bir kicker/temel duruma ihtiyaç duyar. Bu, yönteminizin kendisini sonsuz olarak aramasını durduracak koşuldur. Bu temel durum, karşılaşacağımız en basit durum olarak düşünülebilir. Bu durumda, temel durum dizimizin sonunda olduğumuz zaman olacaktır. Geçerli dizin dizinin uzunluğuna eşitse (diziler 1 değil 0'dan saymaya başladığından eksi 1), sonundayız ve o öğeyi o dizine geri döndürürüz.

Adım 4: Özyinelemeli Adım

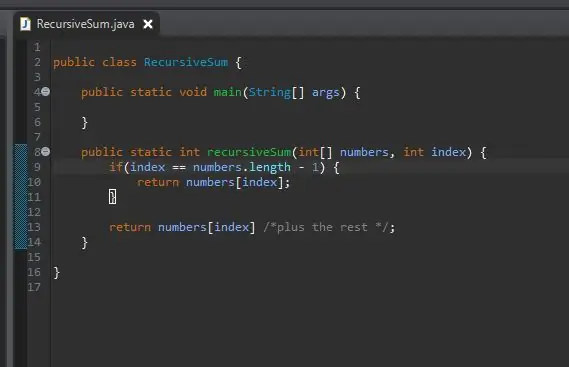
Temel durumumuz olduğunda, bir sonraki adım özyinelemeli adımımızdır. Sihir yapılan yer burasıdır. Dizinimizin dizimizdeki son öğeye eşit olduğu durumu ele aldık. Ya dizimizdeki son elemanda değilsek? Ya şimdiki öğemizi artı bir sonrakini eklemesini söyleyebilirsek? Sonunda dizimizin sonuna ulaşacağız ve temel durumumuz etkili olacak.

Bunu başarmak için, mevcut dizinimizi döndürmemiz ve dizinin "geri kalanını eklememiz" yeterlidir.

Adım 5: Sorunu Kısaltın

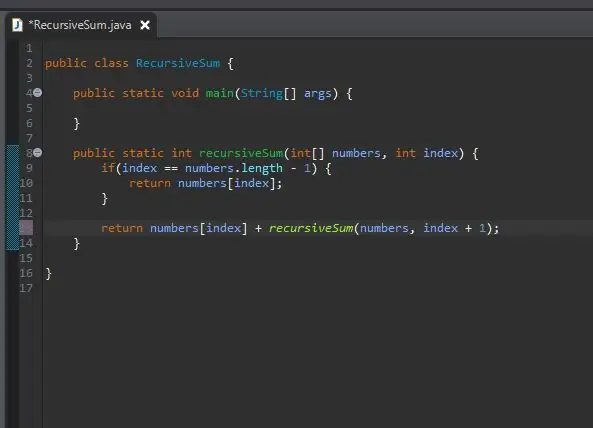
Nasıl basitçe "geri kalanını ekleriz"? Belirli bir öğeyi ekleyecek bir yöntemimiz zaten var; recursiveSum() yöntemimiz! Tekrar çağırabiliriz ama hangi dizini topladığımızı değiştirebiliriz.

İşlediğimiz diziyle aynı diziye geçiyoruz, ancak mevcut dizinimizden sonraki dizine geçiyoruz. Bunu, gösterildiği gibi mevcut dizinimize bir tane ekleyerek yapıyoruz.

Adım 6: Tamsayı Dizisini Oluşturun

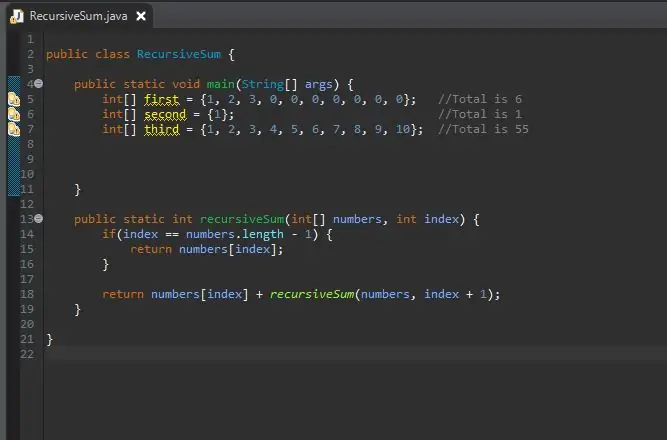
Artık özyinelemeli toplama yöntemimiz tamamlandığında, işleyeceğimiz dizimizi oluşturabiliriz. Bu dizi ana yöntem bloğumuzda olacak.

Dizinin boyutunu istediğiniz kadar yapabilirsiniz. Sadece tek bir boyutta çalışmadığını göstermek için farklı boyut ve değerlere sahip birkaç farklı dizi oluşturdum.

Adım 7: Yöntemi Dizilerinizle Çağırın

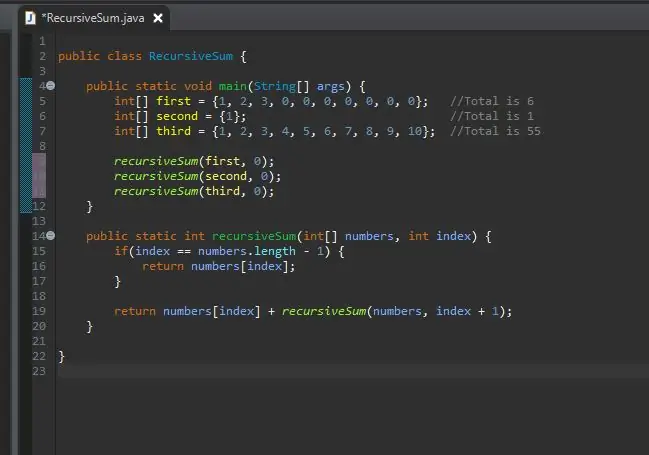
Artık özyinelemeli yönteminizi çağırabilir ve bu dizileri ona iletebilirsiniz. Artık programınızı çalıştırabilirsiniz.

8. Adım: Sonuçları Yazdırın

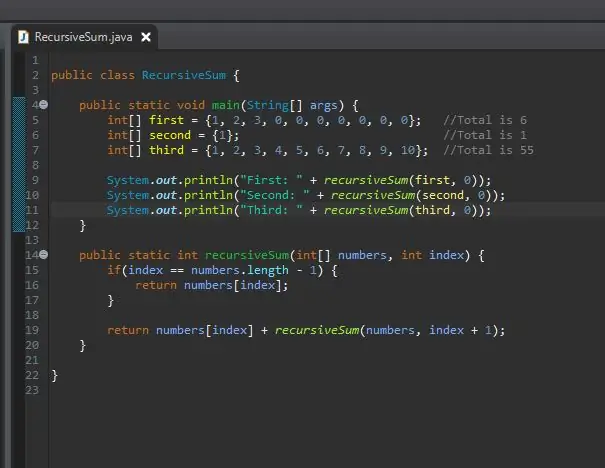
Hiçbir şey olmadı. Niye ya? Özyinelemeli toplam bir tamsayı döndürür, ancak bu tamsayı ile hiçbir şey yapmadık. İşini yaptı ama sonucu göremiyoruz. Sonucu görmek için, basitçe şöyle yazdırıyoruz. Bunu çalıştırdıktan sonra, dizilerinizin her birinin sonuçlarını görmelisiniz.

9. Adım: Tebrikler

Özyinelemeli bir işlevi tamamladınız. Dizilerinizin boyutunu değiştirmekten çekinmeyin. Test ederseniz, boş bir diziniz olduğunda çöktüğünü fark edeceksiniz. Bunu hesaba katmadık ama bu, özyinelemeli yönteminizi geliştirmenin harika bir yolu.