İçindekiler:
- Aşama 1:
- Adım 2:
- Adım 3: Dalga Formları için Gerilim ve Akım Fazör Şeması
- Adım 4: Seri RC Devrelerinin Akım, Direnç ve Gerilim Faz Açıları
- Adım 5: Seri RC Devrelerinin Empedansı ve Faz Açısı
- Adım 6: Empedansın Frekansla Değişimi
- Adım 7: Empedansın ve Faz Açının Frekansla Değişimi
- 8. Adım: Z ve XC'nin Sıklıkla Nasıl Değiştiğinin Bir Resmi
- Yazar John Day day@howwhatproduce.com.
- Public 2024-01-30 13:17.
- Son düzenleme 2025-01-23 15:13.

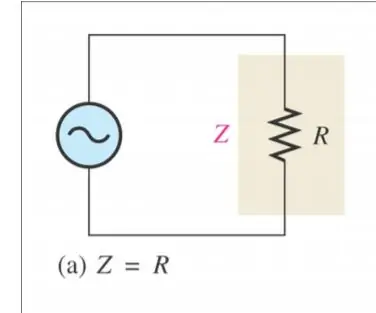
RC devreleri
Empedans: Kaynağın Akım Karşıtlığı olarak "Gördüğü" şeydir
Empedans hesaplama yöntemi bir devreden farklıdır
Aşama 1:

Bir devre tamamen kapasitif olduğunda (yalnızca kapasitör içerdiğinde), uygulanan voltaj ile toplam akım arasındaki faz açısı 90 °'dir (Akım Uçları)
Adım 2:

Bir devrede hem direnç hem de kapasitans kombinasyonu olduğunda, direnç (R) ile kapasitif reaktans (XC) arasındaki faz açısı 90 ° ve toplam empedans (Z) için faz açısı 0 ° ile 90 ° arasındadır
Bir devrede hem direnç hem de kapasitans kombinasyonu olduğunda, toplam akım (IT) ile kapasitör voltajı (VC) arasındaki faz açısı 90 ° ve uygulanan voltaj (VS) ile toplam akım (IT) arasındaki faz açısıdır. Göreceli direnç ve kapasitans değerlerine bağlı olarak 0 ° ile 90 ° arasında bir yerdedir
Adım 3: Dalga Formları için Gerilim ve Akım Fazör Şeması

Adım 4: Seri RC Devrelerinin Akım, Direnç ve Gerilim Faz Açıları

Adım 5: Seri RC Devrelerinin Empedansı ve Faz Açısı

- Seri RC devresinde, toplam empedans, R ve Xc'nin fazör toplamıdır.
- Empedans büyüklüğü: Z = √ R^2 + Xc^2 (Vektör toplamı)
- Faz açısı: θ = tan-1(X C/R)
Neden cebirsel toplam değil vektör toplamını kullanıyoruz?
Cevap: Çünkü Direnç voltajı geciktirmez, ancak Kapasitör bunu yapar.
Yani Z=R+Xc yanlıştır.
Ohm yasasının tüm seri RC devresine uygulanması, Z, Vs ve Itot miktarlarının şu şekilde kullanılmasını içerir:
Itot = Vs/Z Z = Vs/Itot Vs = Itot * Z
Ayrıca şunu da unutmayın:
Xc=1/2πFC
Adım 6: Empedansın Frekansla Değişimi

Adım 7: Empedansın ve Faz Açının Frekansla Değişimi

8. Adım: Z ve XC'nin Sıklıkla Nasıl Değiştiğinin Bir Resmi

R sabit kalır
Önerilen:
Snap Devreleri Telepresence Robotu: 9 Adım

Snap Circuits Telepresence Robot: 2020'deki tatiller biraz farklı. Ailem ülkenin dört bir yanına dağılmış durumda ve pandemi nedeniyle tatillerde bir araya gelemiyoruz. Büyükanne ve büyükbabaları Şükran Günü kutlamamıza dahil etmenin bir yolunu istedim. Bir telepres
MakeyMakey Devreleri: 3 Adım
MakeyMakey Devreleri: Masada makeymakey tahtası, bazı timsah telleri ve bazı elektrik iletken nesneleri karıştırıyoruz. Sıfırdan bazı etkileşimli projelerle, bilgisayarla ve/veya nesnelerle etkileşim kurmak için devreler inşa ediyoruz
ESP32 ve Karakter LCD'li Layad Devreleri Alfanümerik Klavye: 4 Adım

Sıralı Devreler ESP32 ve Karakter LCD'li Alfanümerik Klavye: Bu makale, ESP32'ye veri girmek için bir alfanümerik klavye modülünün ve 16x2 I2C karakterli bir LCD modülünün kullanımını gösterir. Bu yöntem, ESP32'ye Wi-Fi kimlik bilgilerini ve diğer bilgileri girmek ve ESP32'den almak için kullanılabilir
E-tekstil Devreleri için Prototipleme Kiti: 5 Adım
E-tekstil Devreleri için Prototipleme Kiti: Bu talimat, size e-tekstil devrelerini prototiplemek için basit bir kit yapmayı öğretecektir. Bu kit, yeniden kullanılabilir ancak sağlam kablolar ve bağlantı noktalarından oluşur. Bu projenin amacı, e-tekstil ustalarına bir sistem sağlamak
Ses Devreleri için Pasif Düşük Geçiş Filtresi (Serbest Biçimli RC Filtresi): 6 Adım

Ses Devreleri için Pasif Düşük Geçiş Filtresi (Serbest Biçimli RC Filtresi): Özel elektronik enstrümanlar yaparken bana her zaman sorun çıkaran şeylerden biri, ses sinyallerimde sürekli gürültü paraziti olmasıdır. Kablolama sinyalleri için ekranlama ve farklı hileler denedim, ancak kurulum sonrası en basit çözüm
