☠WEEDINATOR☠ Bölüm 4: Diferansiyel Direksiyon Geometrisi Kodu: 3 Adım

2024 Yazar: John Day | [email protected]. Son düzenleme: 2024-01-30 13:21

Yukarıdaki videoyu izleyecek vaktiniz varsa, WEEDINATOR 3 nokta dönüşü yaparken direksiyondaki motorların ara sıra stop etmesinden kaynaklanan bazı garip sesler olduğunu fark edeceksiniz. Dönüş yarıçapı içeriden dışarıya farklı olduğu ve tekerleğin kat ettiği mesafe dönüş derecesi başına farklı olduğu için motorlar esasen birbirine karşı sıkışır.

Dönüşün geometrisi, dönüşün 8 veya daha fazla permütasyonunu çizerek, iç tekerlek üzerinde 0 (dönüşsüz) ila 90 (tam kilit) derece arasında farklı açılarda dönüş örnekleri vererek işlenebilir. Kulağa karmaşık mı geliyor?

Çoğu küçük tekerlekli robot, herhangi bir karmaşık yönlendirmeye sahip olmaya çalışmaz ve çok etkili bir şekilde, aracın her iki tarafındaki motorların göreceli hızını değiştirmeye güvenir; bu, paletli bir kazıcı veya tankın yaptığı ile hemen hemen aynıdır. İşler. Hareket eden her şeye ateş eden krater dolu bir savaş bölgesi üzerinde hücum ediyorsanız bu harikadır, ancak sakin bir tarım ortamında toprağa ve toprağa mümkün olduğunca az zarar vermek önemlidir, bu nedenle taşlama çarkları birbirine karşı ileri geri hareket eder. uygun değil!

Eski Amerikan filmlerinde gördüğünüz ve her köşeyi döndüklerinde lastiklerin deli gibi çığlık attığını duyabileceğiniz arabalar dışında, çoğu araba ve traktörde 'Diferansiyel' adı verilen çok kullanışlı bir alet bulunur. Amerikalılar hala böyle arabalar yapıyor mu? WEEDINATOR ile, herhangi bir dönüş açısında tekerleklerin bağıl hızları ve açıları için formül geliştirerek diferansiyelleri tahrik motorlarına programlayabiliriz. Hala karmaşık geliyor mu?

İşte hızlı bir örnek:

WEEDINATOR bir dönüş yapıyorsa ve iç tekerleği 45 derece ise, dış tekerlek 45 derece DEĞİLDİR, daha çok 30 derece gibidir. Ayrıca, iç tekerlek saatte 1 km'de dönüyor olabilir, ancak dış tekerlek önemli ölçüde daha hızlı olacak, daha çok 1,35 km/saat gibi.

Adım 1: Geometri Kurulumu

Başlangıç için birkaç temel varsayım yapılmıştır:

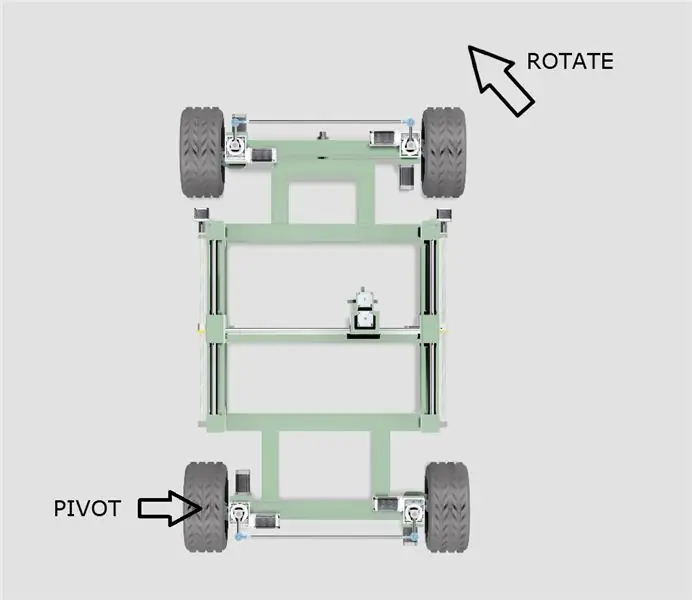
• Şasi, yukarıdaki şemada gösterildiği gibi arka tekerleklerden biri etrafında dönecektir.
• Pivot çemberinin etkin merkezi, dönüş açısına bağlı olarak iki arka tekerleğin merkezinden uzanan bir çizgi boyunca hareket edecektir.
• Geometri bir sinüs eğrisi şeklini alacaktır.

Adım 2: Tekerlek Açılarının ve Yarıçaplarının Ölçekli Çizimleri

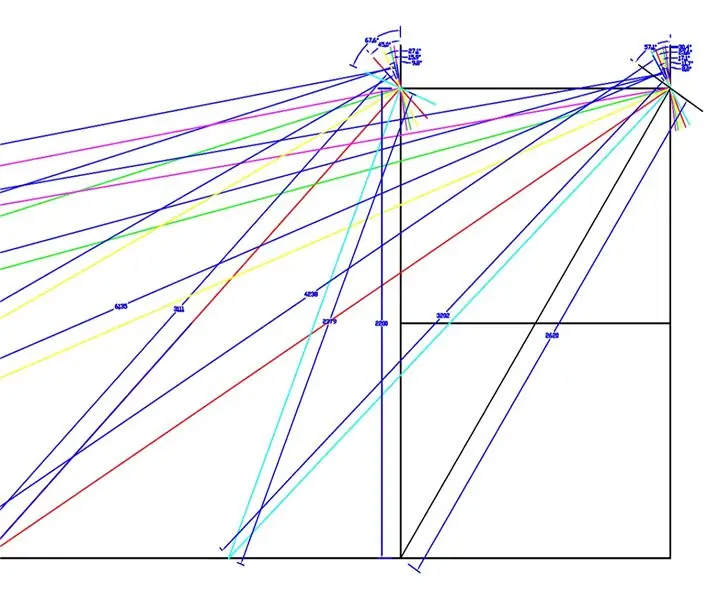
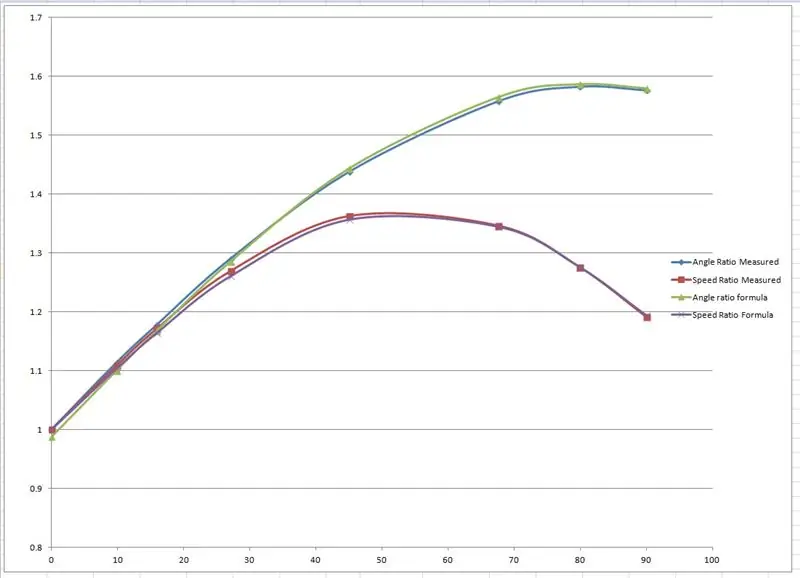
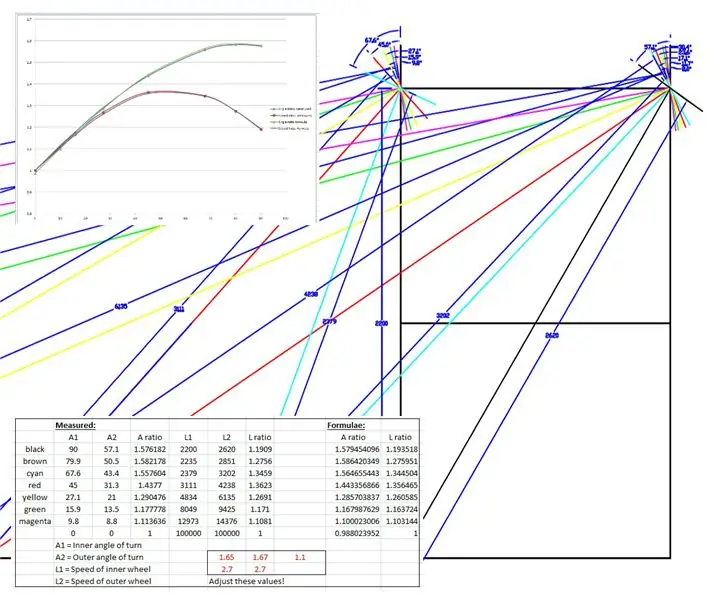
WEEDINATOR ön tekerleklerinin ve şasisinin tam ölçekli bir çizimi 0 ile 90 derece arasında 8 farklı tekerlek iç açısı permütasyonuna sahip şasisi yapılmış ve yukarıdaki çizimlerde gösterildiği gibi ilgili dönüş merkezleri haritalanmıştır.

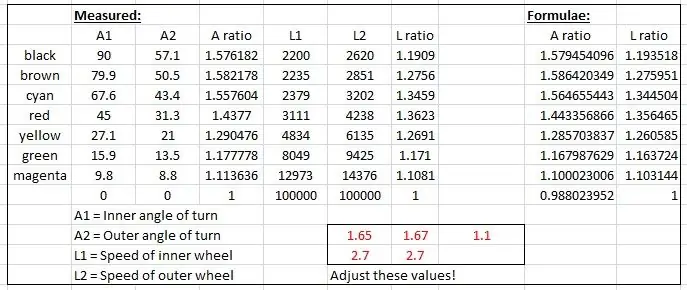
Etkili yarıçaplar çizimden ölçüldü ve Microsoft Excel'de bir grafik üzerinde çizildi.

Biri sol ve sağ ön tekerlek akslarının oranı, diğeri ise her bir dönüş açısı için iki yarıçapın oranı olmak üzere iki grafik üretildi.

Daha sonra sinüs eğrisine dayalı ampirik sonuçları taklit etmek için bazı formüller 'geçirdim'. Fudgelardan biri şuna benziyor:

hızRatio= (sin(iç*1,65*pi/180)+2.7)/2.7; // iç, iç dönüş açısıdır.

Eğriler birbirine uyana kadar excel dosyasında kırmızı ile gösterilen değerler değiştirilerek eğriler düzeltildi.

Adım 3: Formülleri Kodlamak

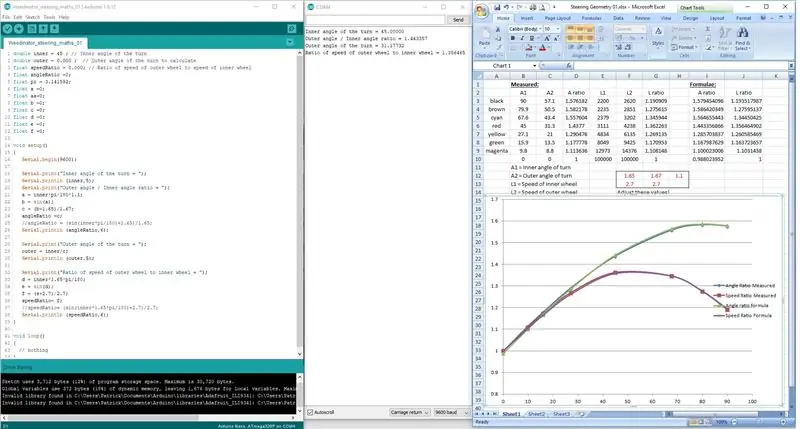
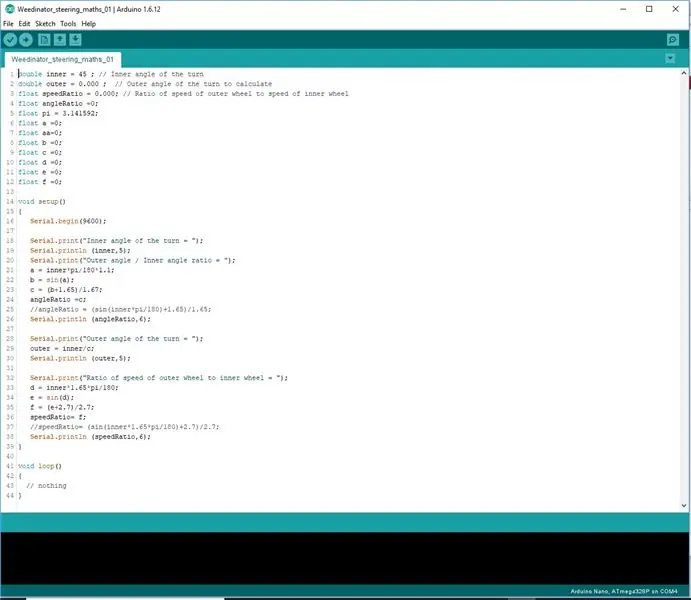
Formülleri tek satırda kodlamaya çalışmak yerine, Arduino'nun matematiği düzgün bir şekilde işlemesini sağlamak için 3 aşamaya bölündüler.

Sonuçlar seri port ekranında gösterilir ve ölçek çiziminde ölçülen sonuçlarla kontrol edilir.