
İçindekiler:
- Yazar John Day day@howwhatproduce.com.
- Public 2024-01-30 13:17.
- Son düzenleme 2025-01-23 15:13.


İşte karmaşık matematik denklemlerinin pratik bir uygulaması.
Bu aslında bileşenleri, hatta bir anteni önceden belirlenmiş frekanslarda karakterize etmek için kullanabileceğiniz çok kullanışlı bir tekniktir.
Elektronikle ilgileniyorsanız, Dirençler ve Ohm yasasına aşina olabilirsiniz. R = V / I Karmaşık empedanslar için de çözmeniz gereken tek şeyin bu olduğunu bilmek sizi şaşırtabilir! Tüm empedanslar özünde karmaşıktır, yani bir Gerçek ve bir Hayali kısma sahiptirler. Bir Direnç durumunda, hayali (veya reaktans) 0'dır, buna bağlı olarak V ve I arasında faz farkı yoktur, bu yüzden onları dışarıda bırakabiliriz.
Karmaşık sayılar hakkında hızlı bir özet. Karmaşık, basitçe, sayının gerçek ve hayali olmak üzere iki kısımdan oluştuğu anlamına gelir. Karmaşık sayıları temsil etmenin iki yolu vardır, örneğin yukarıdaki şekilde bir nokta, sarı ve mavi çizgilerin birleştiği yer gibi Gerçek ve Hayali değerlerle tanımlanabilir. Örneğin mavi çizgi X ekseninde 4, Y ekseninde 3 olsaydı bu sayı 4 + 3i olurdu, i bunun bu sayının sanal kısmı olduğunu belirtir. Aynı noktayı tanımlamanın başka bir yolu da kırmızı çizginin uzunluğu (veya genliği) ve yatayla yaptığı açıdır. Yukarıdaki örnekte bu 5 < 36.87 olacaktır.
Veya 36,87 derecelik bir açıyla 5 uzunluğunda bir çizgi.
Tüm parametrelerin üzerindeki denklemde, R, V ve I hayali bir kısma sahip olarak düşünülebilir, dirençlerle çalışırken bu değer 0'dır.
İndüktörler veya kapasitörler ile çalışırken veya sinyaller arasında bir faz farkı (derece olarak) ölçülebildiğinde, denklem aynı kalır ancak sayının Sanal kısmı dahil edilmelidir. Çoğu bilimsel hesap makinesi karmaşık matematikle çalışmayı çok kolaylaştırır, bu derste bir Casio fx-9750GII üzerinde bir örnek üzerinden çalışacağım.
İlk olarak, direnç voltaj bölücü denkleminin bir özeti.
Şekile göre -
Y'deki voltaj, R2 ile çarpılan akımdır.
i, X voltajının R1 ve R2 toplamına bölümüdür
R2 bilinmediğinde, diğer X, Y, R1 değerlerini ölçebilir ve denklemi R2'yi çözmek için yeniden düzenleyebiliriz.
Gereçler
Bilimsel hesap makinesi
sinyal üreteci
Osiloskop
Adım 1: Kurulum

Test Edilen Cihazın (DUT) endüktansını 1MHz'de hesaplamak istediğimizi varsayalım.
Sinyal üreteci, 1MHZ'de 5V sinüzoidal çıkış için konfigüre edilmiştir.
2k ohm dirençler kullanıyoruz ve osiloskop kanalları CH1 ve CH2
Adım 2: Osiloskop

Şekilde gösterildiği gibi dalga formlarını alıyoruz. Osiloskopta 130ns önde olacak bir faz kayması görülebilir ve ölçülebilir. Genlik 3.4V'dir. Not, CH1 üzerindeki sinyal voltaj bölücünün çıkışında alındığı için 2.5V olmalıdır, burada hesaplarımızda da kullanmamız gereken değer olduğu için netlik için 5V olarak gösterilmiştir. yani 5V, bilinmeyen bileşenli bölücüye giriş voltajıdır.
Adım 3: Aşamayı Hesaplayın

1MHz'de giriş sinyalinin periyodu 1us'tur.
130ns, 0.13'lük bir oran verir. Veya %13. 360'ın %13'ü 46.6'dır
5V sinyaline 0.. açısı verilir, çünkü bu bizim giriş sinyalimizdir ve faz kayması buna göredir.
3.4V sinyaline +46.6'lık bir açı verilir (+, önde olduğu anlamına gelir, bir kapasitör için açı negatif olacaktır).
4. Adım: Hesap Makinesinde


Şimdi sadece ölçülen değerlerimizi hesap makinesine giriyoruz.
R, 2k
V, 5'tir (DÜZENLE - V 5'tir, daha sonra denklemde X kullanılır!
Y, faz açısı ile ölçülen voltajımızdır, bu sayı sadece hesap ekranında gösterildiği gibi açıyı belirterek karmaşık bir sayı olarak girilir.
Adım 5: Denklemi Çözün

şimdi denklem
(Y * R) / (X - Y)
hesap makinesine yazılır, bu tam olarak direnç voltaj bölücülerini çözmek için kullandığımız denklemin aynısıdır:)
Adım 6: Hesaplanan Değerler


Hesap makinesi sonucu verdi
18 + 1872i
18, empedansın gerçek kısmıdır ve 1MHz'de +1872 endüktansına sahiptir.
İndüktör empedans denklemine göre 298uH'ye kadar çalışır.
18 ohm, bir multimetre ile ölçülecek olan dirençten daha yüksektir, bunun nedeni multimetrenin DC'de direnci ölçmesidir. 1MHz'de, iletkenin iç kısmının akım tarafından baypas edildiği ve sadece bakırın dışından aktığı, iletkenin çapraz alanını etkin bir şekilde azaltan ve direncini artıran bir cilt etkisi vardır.
Önerilen:
ESP8266 ESP-12E UART Kablosuz WIFI Kalkanı TTL Dönüştürücü Karmaşık Olmayan: 5 Adım

ESP8266 ESP-12E UART Kablosuz WIFI Kalkanı TTL Dönüştürücü Karmaşık Olmayan: Bu kılavuz, ESP8266 ESP-12E UART Kablosuz WIFI Kalkanı TTL Dönüştürücüyü satın almış ve Arduino ile nasıl kullanacağını bilmeyen kişilere yardımcı olmak için hazırlanmıştır. Başlangıçta, bu öğretici burada Brezilya'da Portekizce yazılmıştır. elimden geleni yapmaya çalıştım
LTspice Kullanarak Empedansı Ölçme: 4 Adım
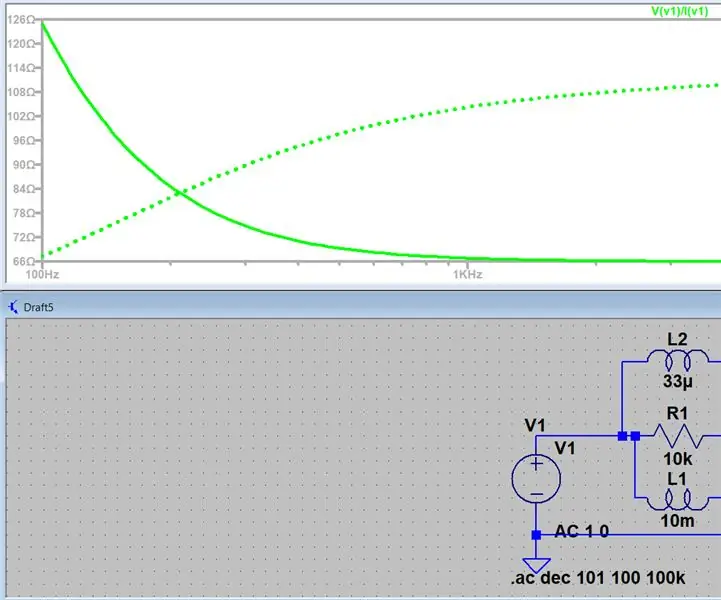
LTspice Kullanarak Empedansı Ölçme: Herkese merhaba, bu, bir devrenin AC taraması oluşturmaya ve herhangi bir noktada empedansı bulmaya basit bir giriş olacak, bu, kurslarımda birkaç kez ortaya çıktı ve benim için herhangi bir şey bulmak çok zordu. çevrimiçi yapmanın yolu yani
Micro:bit Klooikoffer (karmaşık durum): 3 Adım (Resimlerle)

Micro:bit Klooikoffer (karışıklık durumu): Bir pilot olarak kütüphanemiz Micro:bits klooikoffers'ı kiralıyor, bence bu gerçekten harika! Klooikoffer'lar Conrad tarafından sağlanır, ancak bir karton kutu içinde gelirler. Klooikoffer'ları kiralamaya uygun hale getirmek için bazı değişiklikler yaptık
GIMP Kullanarak İnsanları/insanları/hayvanları/robotları Gerçekten Harika/parlak Isı Görüşüne Sahip (Seçtiğiniz Renk) Görünmeleri İçin Gerçekten Basit/Kolay/Karmaşık Olmayan Bir Yo

GIMP Kullanarak İnsanları/insanları/hayvanları/robotları Gerçekten Harika/parlak Isı Görüşüne Sahip (Seçtiğiniz Renk) Görünmeleri İçin Gerçekten Basit/Kolay/Karmaşık Olmayan Bir Yol: Oku…başlığı
Aşırı Karmaşık, Aşırı Mühendislik Yapılmış Pil Yuvası: 13 Adım (Resimlerle)

Süper Aşırı Karmaşık, Aşırı Mühendislik Yapılmış Pil Tutucu…:… gerçekten biraz zamanı olanlar için! Son zamanlardaki harika pil tutucu Instructables döküntüsü, kendi yöntemimi paylaşmam için bana ilham verdi. Bu, birkaç özel araç ve el becerisi gerektirir, ancak eminim ki çok sayıda Instructabler vardır'
