Autodesk Inventor'da Temcor Tarzı Jeodezik Kubbe Nasıl Oluşturulur: 8 Adım

2024 Yazar: John Day | [email protected]. Son düzenleme: 2024-01-30 13:20

Bu eğitim size sadece biraz matematik kullanarak Temcor tarzı bir kubbenin nasıl oluşturulacağını gösterecektir.

Bu eğitimdeki bilgilerin çoğu, TaffGoch'un eski Amundsen-Scott Güney Kutbu İstasyonunun alt bölme yönteminin tersine mühendisliğinden toplanmıştır, bu yüzden ona çok teşekkür ederiz!

Temcor kubbelerinin önemli bir avantajı, düşük benzersiz payanda sayısıdır - Duncan Stuart'ın düzenli triacontahedral jeodezik ızgarasından (Yöntem 3*) farklı olarak, frekansla aritmetik olarak artar, ancak sonuç çok daha hoş görünür.

Basitlik için, yaptığımız kubbenin frekansı 14'tür, bu nedenle kiriş faktörleri TaffGoch'un Temcor modeline göre çapraz kontrol edilebilir.

Inventor 2016.ipt, öğreticinin sonuna eklenmiştir.

*GÜNCELLEME*

Yöntem 4'ü Duncan Stuart'ın düzenli triacontahedral jeodezik ızgarası olarak tanımladım, ama değil. Yöntem aslında, 1985 tarihli makalesi "Geodezik Kubbeler" de yapımını anlatan Christopher Kitrick tarafından icat edildi. Buna ek olarak, 1990 tarihli "A Unified Approach to Class I, II & III Geodesic Domes" adlı makalesinde, biri Duncan Stuart'ın Yöntem 3'ü, diğeri kendi Yöntem 4'ü ve şaşırtıcı bir şekilde, diğer 8 yöntemi özetlemektedir. yeterli, Temcor'un "Yöntem aa" olarak adlandırdığı benzer bir yöntem (Adım 7, Temcor'un "Yöntem aa"yı nasıl değiştirdiğini gösterir). Gelecekteki bir talimatta, ikinci makalede özetlenen yöntemlerin yapısını anlatacağım.

Adım 1: Kullanıcı Parametreleri

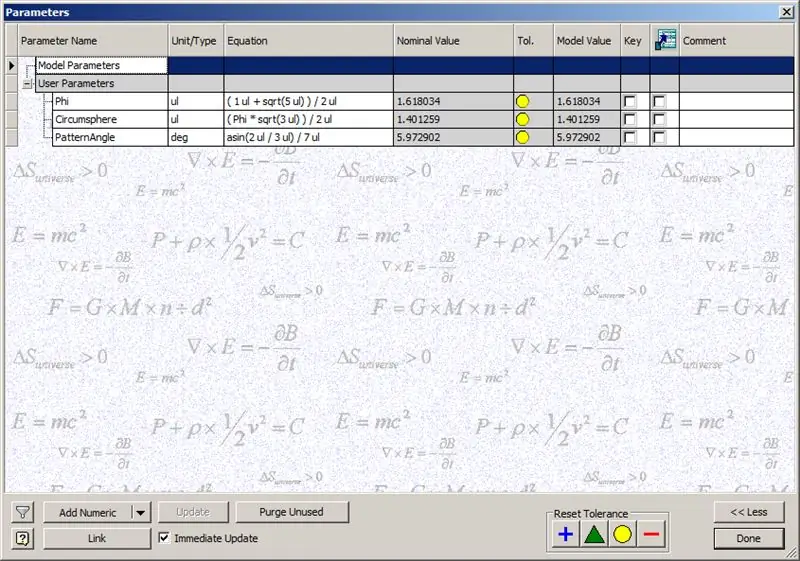
Kubbeyi oluşturmaya başlamadan önce gösterilen parametreleri girin:

Phi - Altın Oran. ((1+√5/)2 olarak tanımlanır

Circumsphere - Bu, ((Phi*√3)/2) olarak tanımlanan bir dodekahedron'un çevresidir.

PatternAngle - Bu, bir dodecahedronun merkez açısıdır. Kubbemizin frekansı 14 olduğundan, bu merkez açıyı frekansın yarısına, bu durumda 7'ye bölüyoruz.

Adım 2: Altın Bir Dikdörtgen Çizmek

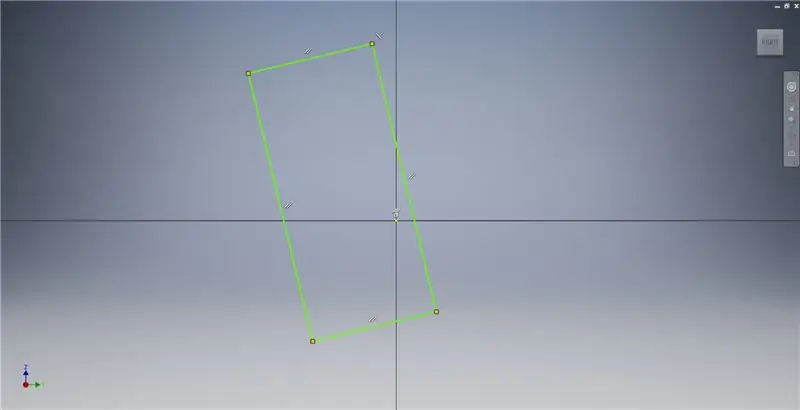
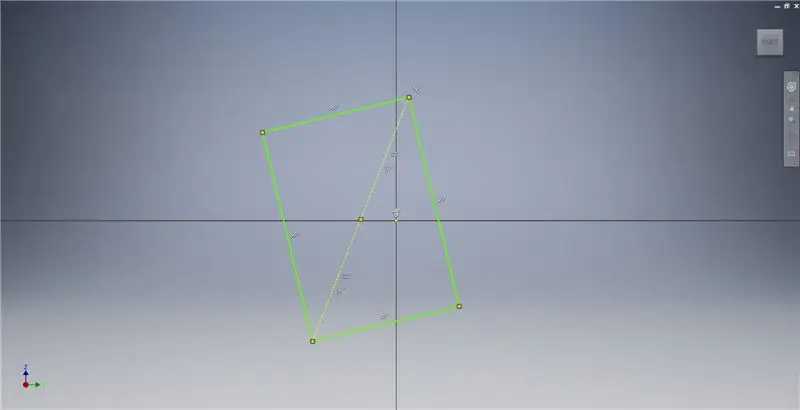
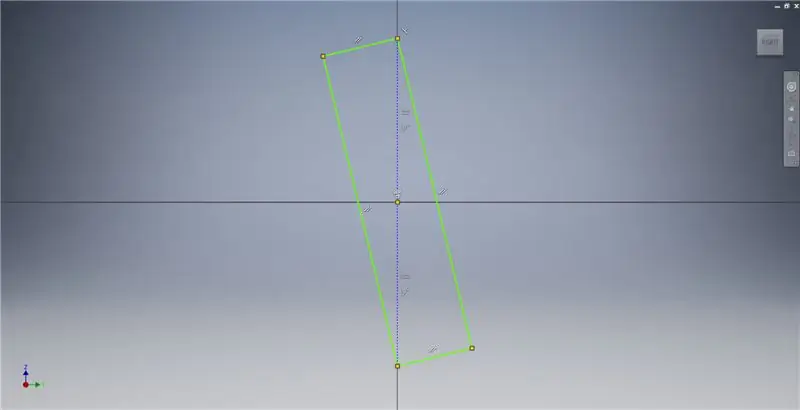
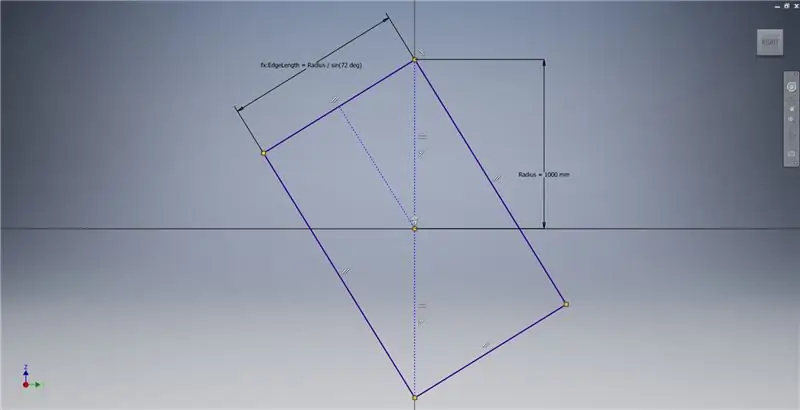
YZ düzleminde bir çizim başlatın, ardından Altın Dikdörtgen oluşturulmasını açıklayan ek bilgiler için resim notlarına bakarak gösterildiği gibi üç noktalı bir dikdörtgen oluşturun.

Adım 3: Golden² Dikdörtgeni Oluşturma

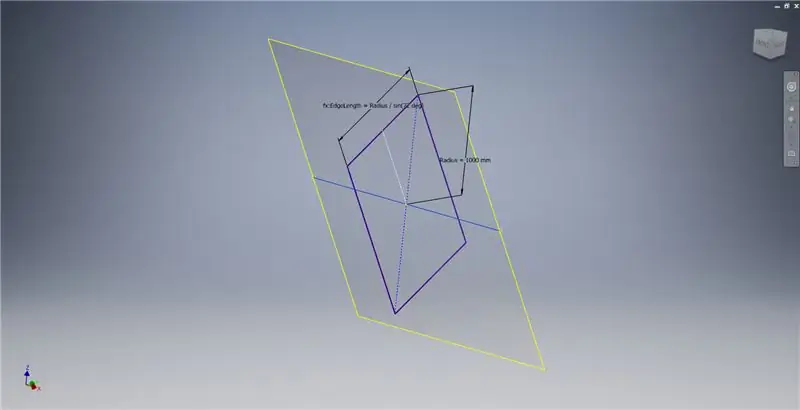
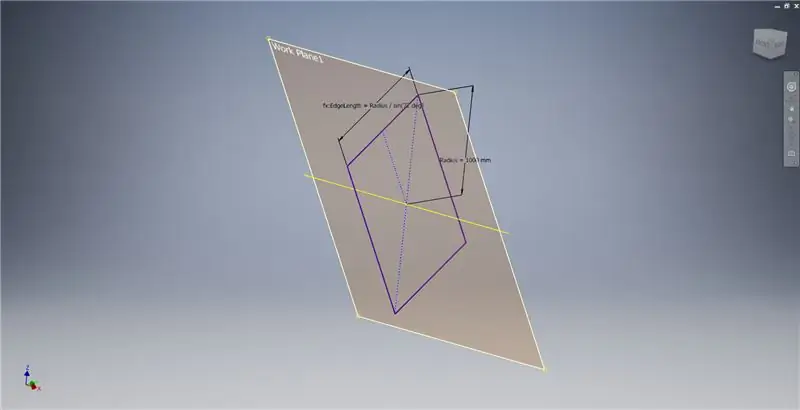
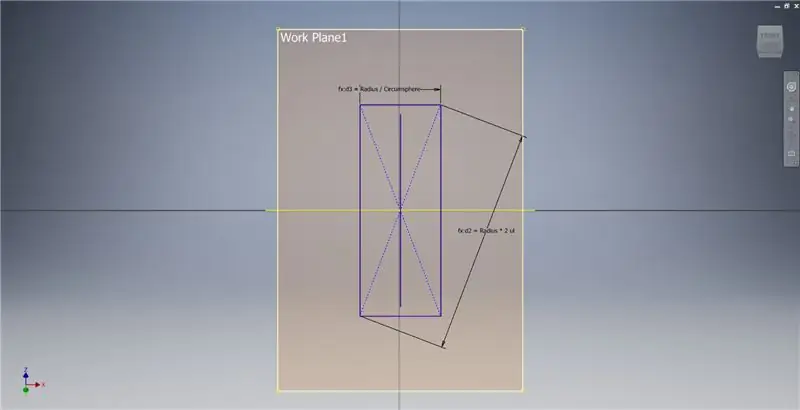
X eksenini ve ilk görüntüde vurgulanan çizgiyi kullanarak bir çalışma düzlemi oluşturun, ardından bu çalışma düzleminde başka bir çizim başlatın. Orijinden başlayarak bir merkez noktası dikdörtgeni oluşturun, ardından dikdörtgeni üçüncü resimde gösterildiği gibi boyutlandırın.

Adım 4: 2v Triacon Üçgeni Oluşturma

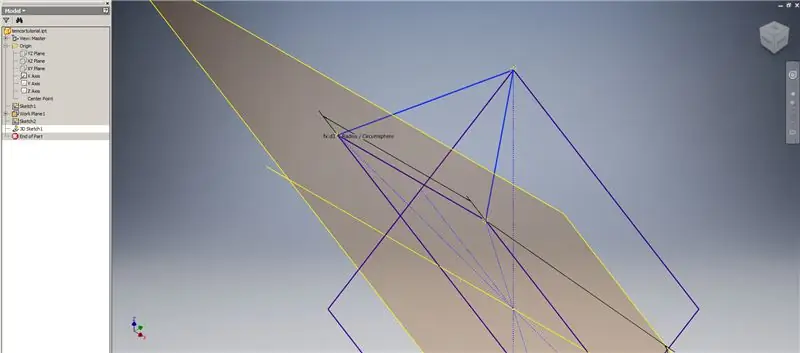
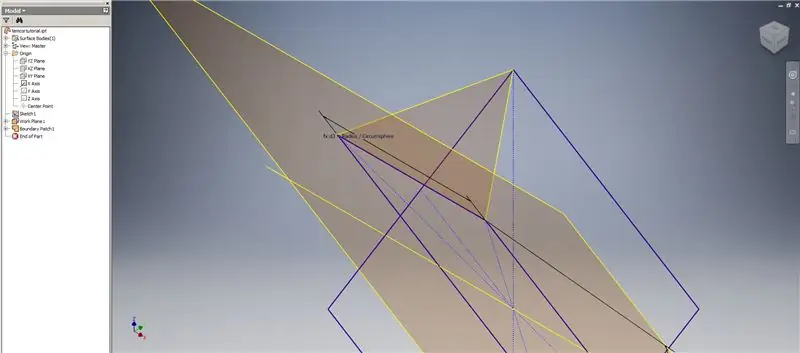
Artık ihtiyacımız olan tüm geometriye sahip olduğumuza göre, tercih ettiğiniz yöntemi kullanarak ikinci görüntüdeki sınır yamasını oluşturun. 3B çizim yapmayı seçtim ama başka bir çalışma düzleminde çizim yapmak da işe yarayabilirdi.

Adım 5: Kavşak Düzlemlerinin Oluşturulması

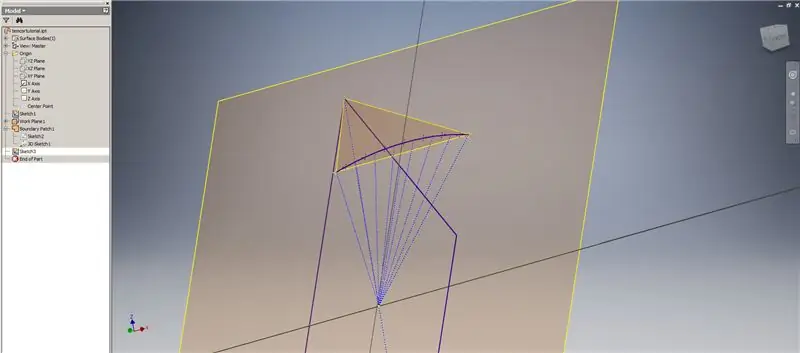
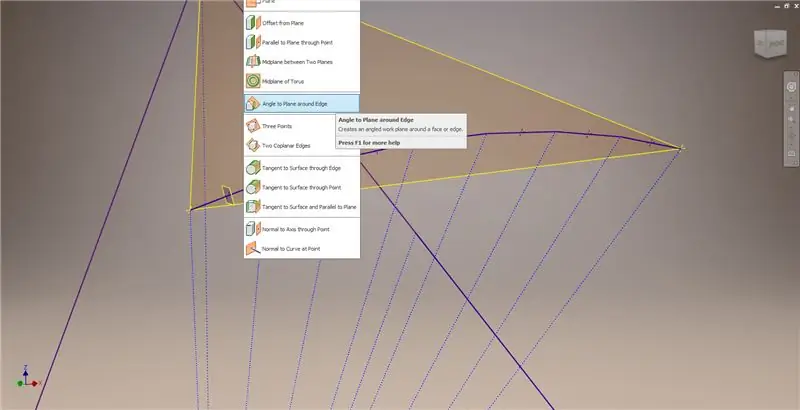
Oluşturduğunuz ilk çalışma düzleminde ("Çalışma Düzlemi 1") başka bir çizim başlatın, Altın² Dikdörtgeninin köşelerini yansıtın, ardından bu noktaları ve orijini 2v triacontahedron'un merkez açısını oluşturmak için bağlayın. Metod 2 arızasını başlatıyormuşsunuz gibi, kubbe frekansının yarısına bölün. Noktaları akorların orta noktalarına yerleştirin.

Çizimden çıkın, ardından ikinci resimde gösterildiği gibi akorlardan birini ve orta noktasını kullanarak bir düzlem oluşturun. Ardından, "Kenarda Açıdan Düzleme" özelliğini kullanarak başka bir çalışma düzlemi oluşturun. Çalışma Düzlemi 1'i ve sağ orta ve sol alt resimde gösterilen inşaat çizgilerinden birini seçin. 90 derecelik varsayılan açıyı kabul edin, aksi takdirde alt bölümün geri kalanı doğru görünmez. Sağ alttaki görüntüde sonucu elde etmek için kalan akorları ve inşaat çizgilerini kullanarak işlemi tekrarlayın.

Adım 6: Kesişme Eğrilerinin Oluşturulması ve Alt Bölmenin Oluşturulması

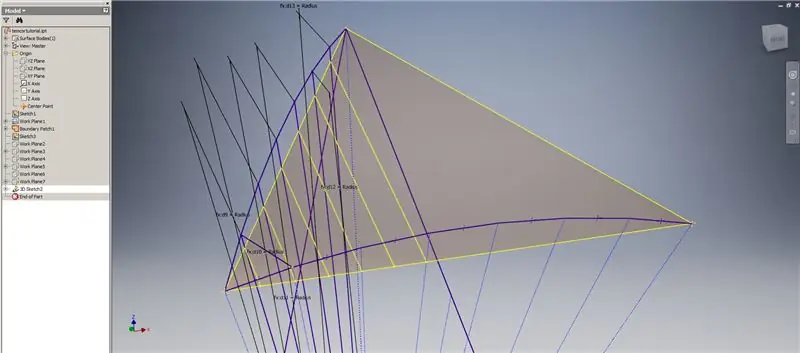
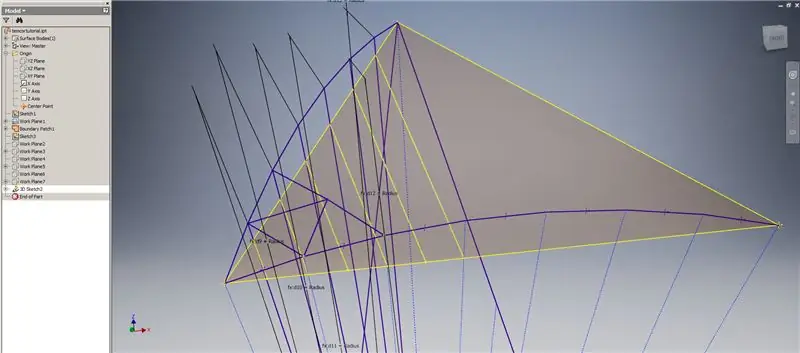
Bir 3B çizim başlatın, ardından az önce oluşturduğunuz çalışma düzlemlerini ve üstteki resimde gösterilen çizgileri oluşturan sınır yamasını kullanarak kesişim eğrileri oluşturun.

Şekil 2'de gösterildiği gibi kesişim eğrilerinin uç noktalarına denk gelen çizgiler çizin. Hepsini kubbenin yarıçapına eşit yapın. Kesişme eğrileri üzerinde uzanan çizgileri birleştiren kirişleri çizin. Alt bölümün bir üçgenini oluşturacak kadar yakın görünen herhangi bir geometriyi bağlayın. Akorların kesişim çalışma düzlemleri boyunca yansıtılacağı sonraki 10 resme bakın - bunu sadece kelimelerden daha iyi açıklayabilirler.

7. Adım: Kubbeyi Tamamlama

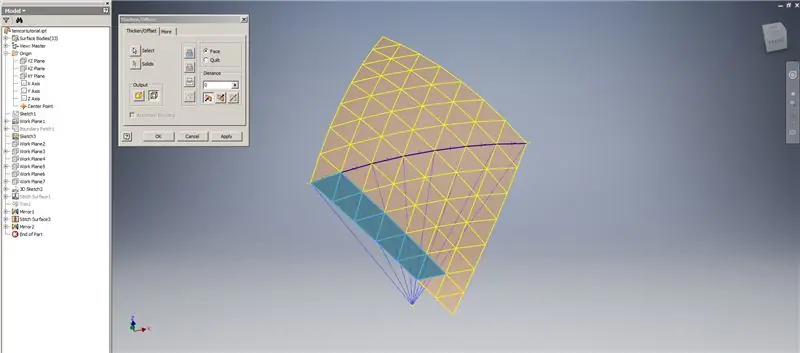
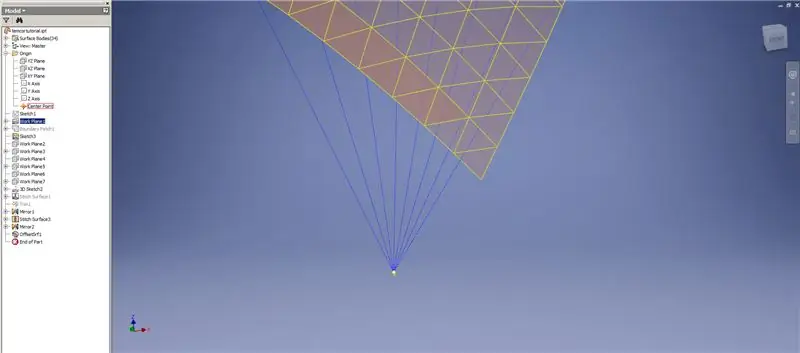
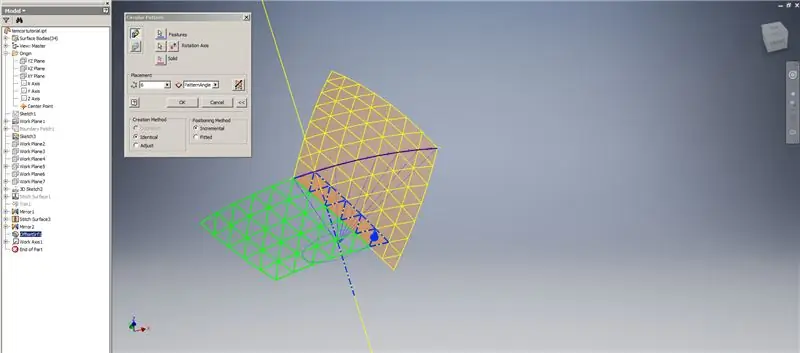
Son iki üçgen sırasını atlayarak, alt sıraların bir Kalınlaştırma/Ofseti oluşturun. Yeni OffsetSrf'yi 6 kez veya ((Frequency=14)/2)-1'i modelleyin. OffsetSrf'i gizleyin, desenli yüzeyleri dikin, ardından dikilen yüzeyi YZ Düzlemi ile aynalayın. Şekil 6'da gösterildiği gibi, üst üçgenin tepe noktalarına dayanan çalışma düzlemleri oluşturun. Bu yeni çalışma düzlemlerini kullanarak dikilmiş ve aynalanmış yüzeyleri kesin, ardından kalan yüzeyleri birbirine dikin. Bu son yüzeyi Z ekseni boyunca desenleyin, ardından bu son yüzeyleri birbirine dikin ve işiniz bitti!

Adım 8: Akorları Kontrol Etme

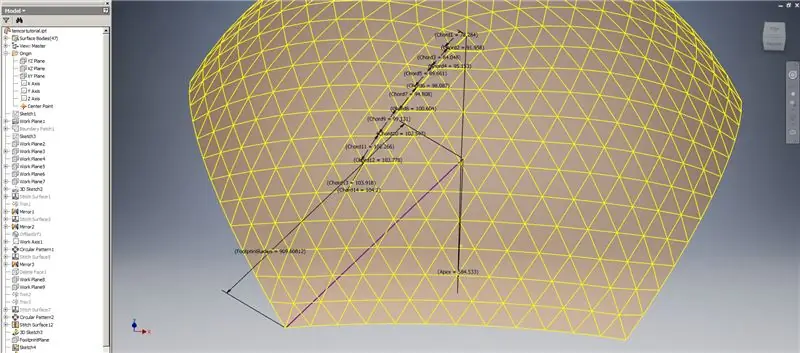
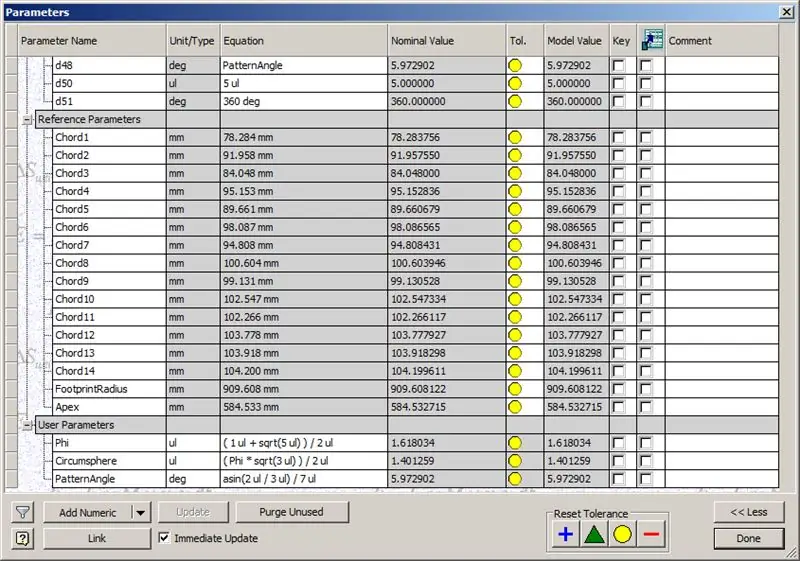
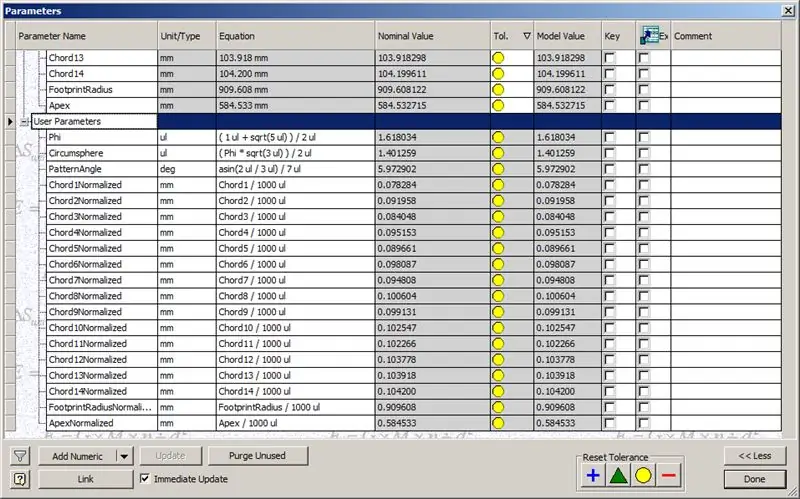
Yani, kubbemiz bitti, ama bakalım sayıların TaffGoch'un modeliyle uyuşup uyuşmadığını görelim:

Referans parametrelerine bakıldığında, mükemmel bir eşleşme oldukları görülüyor!

Kordon uzunluklarını 1000'e bölerek, TaffGoch'un modelinin kiriş faktörlerinin yanı sıra ayak izi yarıçapı ve tepe faktörleri ile mükemmel bir uyum olduğunu açıkça görebiliriz.